回观撒下花籽,五彩缤纷一片——记数学家杨必成: 疫情三年科研成果丰硕

2023年春,肆虐在祖国大地三年的新冠疫情终于划上了句号。回望这段艰难的时光,杨必成教授及其科研团队成员逆境而上,坚持组织好课题研究,日夜笔耕奔忙,终于取得骄人成绩:在已发表的69篇合作论文中,有51篇为SCI收录,2篇在权威期刊,还出版了5本专著,诚可谓硕果累累! 2021年9月18日,杨必成应邀参加了在“北京会议中心”举行的“第十九届中国科学家(国际)论坛”,荣获大会颁发《“十四五”科技强国创新驱动领军人物》证书及奖牌; 同年10月19日,《我是科学人》栏目视频:《杨必成:执于探微,不负数学一生》获挂《学习强国》网站,至今已有超20000人次的阅读记录;2022年10月10日,杨必成光荣入册美国斯坦福大学版“全球前2%顶尖科学家”的“终身影响力排行版(1960-2021年)”榜单。
一、发表成果(论文69篇,专著5本):
(1)英文论文(51篇,SCI收录):
Bicheng Yang, Shanhe Wu and Jianquan Liao. On a new extended Hardy-Hilbert’s inequality with parameters. Mathematics, 2020,8,73; doi:10.3390/ math8010073. (中译题目《关于一个推广的含参数Hardy-Hilbert不等式》)
Bing He and Bicheng Yang. A Mulholland-type inequality in the whole plane with multi parameters. Journal of King Saud University–Science , 2020, 32, 245-250. (中译题目《一个全平面含参数的Mulholland型不等式》)
Hongmin Mo and Bicheng Yang. On a new Hilbert-type integral inequality involving the upper limit functions. Journal of Inequalities and Applications (2020) 2020:5. (中译题目《一个新的涉及可变上限函数的Hilbert型积分不等式》)
Xing Shou Huang, Ricai Luo and Bicheng Yang. On a new extended half-discrete Hilbert’s inequality involving partial sums. Journal of Inequalities and Applications (2020) 2020:16.(中译题目《关于一个新的推广的涉及部分和的半离散Hilbert不等式》)
Bicheng Yang, Shanhe Wu and Qian Chen, On an extended Hardy-Littlewood -Polya’s inequality. AIMS Mathematics, 2020, 5(2), 1550-1561.(中译题目《关于一个推广的Hardy-Littlewood-Polya不等式》)
Jianqua Liao, Shanhe Wu and Bicheng Yang. On a new half-discrete Hilbert-type inequality involving the variable upper limit integral and the partial sum. Mathematics, 2020,8,229; doi:10.3390/math8020229. (中译题目《关于一个新的涉及可变上限积分与部分和的半离散Hilbert型不等式》)
Bicheng Yang, Meifa Huang, and Yanru Zhong. Equivalent statements of a more accurate extended Mulholland’s inequality with a best possible constant factor. Mathematical Inequalities and Applications , 2020, 23(1),231-244.(中译题目《一个较为精确推广的具有最佳常数因子的Mulholland不等式的等价描述》)
Bicheng Yang, Shanhe Wu and Aizhen Wang. A new Hilbert-type inequality with positive homogeneous kernel and its equivalent form. Symmetric , 2020, 12, 342; doi:10.3390/ sym12030342 (中译题目《一个新的具有正齐次核的Hilbert型积分不等式及其等价式》)9.Zhenxiao Huang, Yanping Shi and Bicheng Yang. On a reverse extended Hardy-Hilbert’s inequality. Journal of Inequalities and Applications (2020), 2020:68. (中译题目《关于一个逆向推广的Hardy-Hilbert不等式》)
10.M. Th. Rassias, B.C. Yang and A. Raigorodskii. On Hardy-type integral inequality in the whole plane related to the extended Hurwitz-zeta fanction. Journal of Inequalities and Applications (2020), 2020: 94. (中译题目《一个全平面联系推广的Hurwitz-zeta 函数的Hardy型积分不等式》)
11.Jianqua Liao, Yong Hong and Bicheng Yang. Equivalent conditions of a Hilbert-type multiple integral inequality holding. Journal of Function Spaces, Volume 2020, Article ID 3050952, 6 pages. (中译题目《一个Hilbert型多重积分不等式存在的等价条件》)
12.Aizhen Wang and Bicheng Yang. Equivalent property of a more accurate half-discrete Hilbert’s Inequality . Journal of Applied Analysis and Computation, Volume 10, Number 3, 2020, 920-934. (中译题目《一个较为精确的半离散Hilbert不等式的等价性质》)
13.Yong Hong, Jianqua Liao, Bicheng Yang and Qiang Chen. A class of Hilbert-type multiple integral inequalities with the kernel of generalized homogeneous function and its applications. Journal of Inequalities and Applications (2020), 2020: 140. (中译题目《一类具有一般齐次核函数的Hilbert型多重积分不等式及应用》)
14. Bicheng Yang, Shanhe Wu and Qiang Chen. A new extension of Hardy-Hilbert’s inequality containing kernel of double power functions. Mathematics, 2020,8, 339; doi:10.3390/ math8060894. (中译题目《一个新的推广的包含两个幂函数的Hardy-Hilbert不等式》)
15. M. Th. Rassias, B.C. Yang and A. Raigorodskii. On the reverse Hardy-type integral inequalities in the whole plane with the extended Riemann-Zeta function. Journal of Mathematics Inequalities, 2020, 14(2) : 525 -546. (中译题目《一个逆向的全平面联系推广的Riemann-Zeta函数的Hilbert型积分不等式》)
16. Bicheng Yang and Yanru Zhong. On a reverse Hardy-Littlewood-Polay’s inequality. Journal of Applied Analysis and Computation, Volume 10, Number 5, 2020, 2220-2232. (中译题目《一个逆向的Hardy-Littlewood-Polay不等式》)
17. Weiliang Wu and Bicheng Yang. A few equivalent statements of a Hilbert-type integral inequality with the Reimann-zeta function. Journal of Applied Analysis and Computation, Volume 10, Number 6, 2020, 2400-2417.(中译题目《一个联系Riemann-Zeta函数的Hilbert型积分不等式的几个等价陈述》)
18. Zhaohui Gu and Bicheng Yang. On an extended Hardy-Hilbert’s inequality in the whole plane. Journal of Applied Analysis and Computation, Volume 10, Number 6, 2020, 2619-2630.(中译题目《一个全平面联系推广的Hardy-Hilbert不等式》)
19. Qiang Chen and Bicheng Yang. A reverse Hardy–Hilbert-type integral inequality involving one derivative function. Journal of Inequalities and Applications (2020), 2020: 259. (中译题目《一个逆向的涉及导函数的Hardy-Hilbert积分不等式》)
20. Qiang Chen and Bicheng Yang. On a parametric more accurate Hilbert-type inequality. Journal of Mathematical Inequalities, 2020, 14(4) : 1135 -1149. (中译题目《关于一个较为精确的参量化Hilbert型不等式》)
21.Aizhen Wang and Bicheng Yang. Equivalent statements of a Hilbert-type integral inequality with the extended Hurwitz zeta function in the whole plane. Journal of Mathematical Inequalities, 2020, 14(4) : 1039 -1054.(中译题目《一个联系推广的Hurwitz zeta函数的全平面Hilbert型不等式的等价陈述》)
22. M. Th. Rassias, B.C. Yang and A. Raigorodskii. On a more accurate reverse Hilbert-type inequality in the whole plane. Journal of Mathematical Inequalities, 2020, 14(4) : 1359 -1374.(中译题目《一个较为精确逆向的全平面Hilbert型不等式》)
23. Xingshou Huang and Bicheng Yang.On a more accurate Hilbert-type inequality in the whole plane with the general homogeneous kernel. Journal of Inequalities and Applications (2021), 2021: 10. (中译题目《一个较为精确的全平面Hilbert型不等式》)
24. Michael Th. Rassias, Bicheng Yang and Andrei Raigorodsii. A Hilbert-type integral inequality in the whole plane related to the Arc tangent function. Symmetry 2021, 13, 351. (中译题目《一个联系反正切函数的全平面Hilbert型积分不等式》)
25. Ricai Luo, Bicheng Yang and Xingshou Huang, On a reverse Mulholland-type inequality in the whole plane with general homogeneous kernel. Journal of Inequalities and Applications (2021), 2021: 46. (中译题目《一个具有一般齐次核的全平面逆向Mulholland 不等式》)
26. Qiliang Huang, Bicheng Yang. On a more accurate Hardy-Hilbert’s inequality in the whole plane. Int. J. Nonlinear Anal. Appl. 12 (2021) No. 1, 1167-1179. (中译题目《一个较为精确的全平面Hardy-Hilbert 不等式》)
27. Jianghua Zhong and Bicheng Yang. On a multiple Hilbert-type integral inequality involving the upper limit functions. Journal of Inequalities and Applications (2021), 2021: 17.(中译题目《一个多重的联系可变上限函数的Hilbert型积分不等式》)
28. M. Th. Rassias, B. C. Yang and A. Raigorodskii. Equivalent properties of two kinds of Hardy-type integral inequalities. Symmetry 2021, 13, 1006. (中译题目《两类Hardy型积分 不等式的等价性质》)
29. Bing He , Yong Hong, Zhen Li and Bicheng Yang . Necessary and sufficient conditions and optimal constant factors for the validity of multiple integral half-discrete Hilbert type inequalities with a class of quasi-homogeneous kernels. Journal of Applied Analysis and Computation, 2021,11(1), 521-531. (中译题目《联系多重半离散Hilbert型积分不等式具有最佳常数因子的等价条件》)
30. Bicheng Yang, Shanhe Wu and Aizhen Wang. A new reverse Mulholland-type inequality with multi-parameters. AIMS Mathematics, 2021, 6(9), 9939-9954. (中译题目:《一个联系多参数的新的逆向Mulholland 不等式》)
31.Michael Th. Rassias, Bicheng Yang , Gerasimos C. Meletiou. A more accurate half-discrete Hilbert-type inequality in the whole plane and the reverses. Ann. Funct. Anal. (2021) 12:50. (中译题目:《一个较为精确的全平面半离散Hilbert 型不等式及其逆式》)
32. Qiang Chen and Bicheng Yang. On two kinds of the reverse half-discrete Mulholland -type inequalities involving higher-order derivative function. Journal of Inequalities and Applications (2021), 2021: 138. (中译题目:《关于两类涉及高阶导函数的半离散逆向的Mulholland 型不等式》)
33. Xianyong Huang, Shanhe Wu and Bicheng Yang. A more accurate half-discrete Hilbert-type inequality involving one upper limit function and one partial sums. Symmetric, 2021,13, 154。(中译题目:《一个涉及高阶可变上限函数及部分和的较为精确半离散Hilbert 型不等式》)
34. Bicheng Yang , Michael Th. Rassias, and Andrei Raigorodskii. On an extension of a Hardy -Hilbert-type inequality with multi-parameters. Mathematics, 2021, 9, 2432. (中译题目:《关于一个具有多参数的推广的Hardy-Hilbert 型不等式》)
35. Bicheng Yang, Yanru Zhong and Aizhen Wang. On a new Hilbert-type inequality in the whole plane with the general homogeneous kernel. Journal of Applied Analysis and Computation, 2021, 11(5): 2583– 2600. (中译题目:《一个新的具有一般齐次核的全平面Hilbert 型不等式》)
36. Bicheng Yang, Shanhe Wu and Xingshou Huang. A Hardy–Hilbert-type inequality involving parameters composed of a pair of weight coefficients with their sums. Mathematics 2021, 9, 2950. (中译题目:《一个涉及参数组合一对和的权系数的Hardy-Hilbert 型不等式》)
37. Zhaohui Gu and Bicheng Yang. An extended Hardy-Hilbert’s inequality with parameters and applications. Journal of Mathematical Inequalities, 2021, 15(4) : 1375 -1389. (中译题目:《一个联系参数推广的Hardy-Hilbert不等式及应用》)
37. Bing He, Yanru Zhong and Bicheng Yang. On a more accurate Hilbert-type Inequality involving the partial sums. Journal of Mathematical Inequalities, 2021, 15(4) : 1647 -1662. (中译题目:《一个涉及部分和的较为精确的Hilbert 型不等式》)
38. Jianquan Liao, Shanhe Wu , and Bicheng Yang. A multi parameter Hardy –Hilbert-type inequality containing partial sums as the terms of series. Journal of Mathematics, Volume 2021, Article ID 5264623, 11 pages. (中译题目:《一个包含部分和为级数项的多参数Hilbert 型不等式》)
39. Xianyong Huang and Bicheng Yang. On a more accurate half-discrete Mulholland-type inequality involving one multiple upper limit function. Journal of Function Spaces Volume 2021, Article ID 6970158, 9 pages. (中译题目:《一个涉及多重可变上限的较为精确半离散Mulholland型不等式》)
40. Michael Th. Rassias, Bicheng Yang and Andrei Raigorodskii. A new Hardy –Mulholland-type inequality with a mixed kernel. Advances in Operator Theory (2021) 6:27. (中译题目:《一个新的涉及混合核的Hardy-Mulholland型不等式》)
41. Xianyong Huang , Shanhe Wu and Bicheng Yang. A Hardy-Hilbert-type inequality involving modified weight coefficients and partial sums. AIMS Mathematics, 2022,7(4): 6294–6310. DOI: 10.3934/math.2022350.(中译题目:《一个涉及改进的权系数与部分和的Hardy-Hilbert不等式》)
42. Jianhua Zhong, Bicheng Yang and Qiang Chen. A more accurate half-discrete Hilbert-type inequality involving one higher-order derivative function. Journal of Applied Analysis and Computation Volume 12, Number 1, 2022, 378–391.(中译题目:《一个较为精确的涉及一个高阶导函数的半离散Hilbert型不等式》)
43. Aizhen Wang and Bicheng Yang. A reverse more accurate Hardy-Hilbert’s inequality. Journal of Applied Analysis and Computation Volume 12, Number 2, 2022, 720–735. (中译题目:《一个较为精确逆向的Hardy-Hilbert不等式》)
Aizhen Wang, Yong Hong and Bicheng Yang. On a new half-discrete
Hilbert-type inequality with the multiple upper limit function and the partial sums. Journal of Applied Analysis and Computation, Volume 12, Number 2, 2022, 814–830.(中译题目:《一个新的涉及多重可变上限函数及部分和的半离散Hilbert型不等式》)
45. Bicheng Yang, Shanhe Wu and Xingshou Huang. A reverse Hardy-Hilbert’s inequality involving one partial sum as the terms of double series. Journal of Function Spaces, Volume 2022, Article ID 2175463, 9 pages.(中译题目:《一个逆向的涉及部分和作为重级数项的半离散Hardy-Hilbert不等式》)
46. Xingshou Huang , Bicheng Yang and Ricai Luo. A new reverse Hardy–Hilbert inequality with the power function as intermediate variables. Journal of Inequalities and Applications (2022), 2022: 49. (中译题目:《一个新的含幂函数作为中间变量的Hardy-Hilbert不等式》)
47. M. Th. Rassias, B.C. Yang and A. Raigorodskii. Equivalent conditions of a multiple Hilbert -type integral inequality with the non homogeneous kernel. Rev. Real Acad. Cienc. Exact as Fis. Nat. Ser.A-Mat. (2022) 116:107.(中译题目:《一个含非齐次核的多重Hilbert型积分不等式》)
48. Bicheng Yang , Shanhe Wu and Xingshou Huang. A reverse Hardy–Hilbert’s inequality containing multiple parameters and one partial sum. Mathematics 2022, 10, 2362. https://doi.org/10.3390/math10132362.(中译题目:《一个包含多参数及部分和的逆向Hardy-Hilbert不等式》)
49.B. C. Yang, D. Andrica, O. Bagdasar, and M. Th. Rassias . An equivalent property of a Hilbert-type integral inequality and its applications. Appl. Anal. Discrete Math. 16 (2022), 548-563.(中译题目:《一个Hilbert型积分不等式的等价性质及应用》)
50.Qiang Chen, Yong Hong and Bicheng Yang. A more accurate extended Hardy-Hilbert’s inequality with parameters. Journal of Mathematical Inequalities, 2022, 16(3) : 1075 -1089. (中译题目:《一个较为精确联系参数推广的Hardy-Hilbert不等式》)
F.G Wu, Y. Hong and B.C. Yang. A refined Hardy-Littlewood-Polya inequality and the equivalent forms. Journal of Mathematical inequalities, 16(4)(2022).(中译题目:《一个改进的Hardy-Littlewood-Polya不等式及其等价式》)
(2) 国内论文(14篇,其中权威期刊2篇,核心期刊5篇)
1.廖建全,杨必成.关于一个引入中间变量的一般非齐次核全平面Hilbert型积分不等式,数学学报, 2020,63(1):27-44.(权威期刊)
2.黄启亮,杨必成.具有一般齐次核多维的半离散Hardy-Hilbert型不等式,数学学报, 2020,63(5):427-442.(权威期刊)
3.黄启亮,杨必成.一般齐次核 Hardy-Mulholland 型不等式.浙江大学学报(理),2020,47(3):306-311.
4.辛冬梅,杨必成. 一个较为精确的加强型的半离散Hilbert型不等式.吉林大学 学报(理) , 2020,58(2):225-230.
5.杨必成. Hardy 型积分不等式的等价性质及其应用,广东第二师范学院学报,2020, 40(3): 1-11.
6.杨必成.一个非齐次核较为精确半离散的Hilbert型不等式的等价性质. 广东第二师范学院学报,2020,40(5): 1-9.
7.辛冬梅,杨必成.关于逆向Hilbert型积分不等式的 一组等价陈述.广东第二师范学院学报,2020,40(5): 28-36.
8.杨必成.一个多维逆向的Hilbert型积分不等式的等价陈述.东莞理工学院学报,2021, 38 (3),1-7.
9.杨必成.一个涉及多重可变上限函数的半离散Hilbert型不等式.东莞理工学院 学报,2021, 38(5),1-8.
10.王爱珍,杨必成.非齐次核半离散Hilbert型不等式的等价性质.东莞理工学院学报,2021, 38(5),9-13.
11.辛冬梅,杨必成,闫志来.具有一个导函数的 Hardy-Hilbert型积分不等式.吉林大学学报(理),2021,39(6),1380-1386.
12.吴善和,黄先勇,杨必成.一个涉及多重可变上限函数的半离散Hardy -Mulholland 型不等式.华南师范大学(自),2022,54(1),100-106.
13.王爱珍,杨必成.一个新的涉及高阶导函数的半离散 Hilbert型不等式。吉林大学学报(理),2022,60(2),240-246.
14.辛冬梅,杨必成,一个加强的 Hilbert型不等式。五邑大学学报(自),2022,36 ,63-67.
(3)参编论文(2本含4篇):
1.Trigonometric Sums and Their Applications (Ed. Andrei Raigorodskii, Michael Th. Rassias),Springer, 2020.
(i)Michael Th. Rassias, Bicheng Yang, On a Half-Discrete Hilbert-Type Inequality in the whole plane with the kernel of hyperbolic secant function related to the Hurwitz zeta function. (ii) Bicheng Yang. Equivalent conditions of a reverse Hilbert-type integral inequality with the kernel of hyperbolic cotangent function related to the Riemann zeta function.
2. 不等式研究(三),哈尔滨 工业大学出版社,2022.
(iii)杨必成。关于一个加强逆向的 Hilbert型不等式。
(iv)杨必成。一个加强逆向的 Hardy-Littlewood-Polya 不等式。
专著(5本):
(1)Bicheng Yang, Jianquan Liao. Parameterized Multidimensional Hilbert-Type Inequalities (40万字),Scientific Research Publishing, USA 2020.
(2)Bicheng Yang, Jianquan Liao, Ravi P. Agarwal. Hilbert-Type Inequalities: Operators, Compositions and Extensions (45万字), Scientific Research Publishing, USA 2020.
(3)杨必成,黄启亮。Hilbert型不等式。(约16万字),哈尔滨工业大学出版社,2020。
(4)Bicheng Yang and Ricai Luo. Hilbert-Type and Hardy-Type Integral Inequalities in the Whole Plane . Scientific Research Publishing, 2022, USA.(中译题目:《全平面的Hilbert型不等式》)
(5) Bicheng Yang and Michael Th. Rassias。On Extended Hardy–Hilbert Integral Inequalities and Applications。World Scientific Publishing Co. Ptc.Ltd.2022, Singapore.(中译题目:《论推广的Hardy-Hilbert积分不等式及应用》)

二.媒体褒扬 (27项)
1.2020年1月,入册《祖国赞歌(第二卷)》(326-327页),并编入该书唯一封 面人物 (中 国文联出版社,刘旭东主编)。
2.2020年4月,入册《中国影响力人物》(90页)(中国未来研究会科技分会编)。
3.2020年8月15日,获汕尾中学“鸣谢”牌匾(捐赠5万元予“汕尾中学2020 高考优胜奖”10人).
4.2020年10月25日,《汕尾日报》載文《自由探秘 成绩雯然——记创立Yang-Hilbert型不等式理论的杨必成教授》,《今日头条》转载。
5.2020年10月21-22日,《今日头条》转载《杨必成教授在汕尾中学120周年校庆大会上的讲话》及《贺杨必成教授七十四寿诞:诗及花絮》。
6.2020年11月2日,《中国改革报》載文《砥砺前行,探秘洞悉数学堂奥——记创立Yang-Hilbert型不等式理论的杨必成教授》。
7.下面为转载《中国改革报》上文的21个网站(2020.12.24):
人民日报 中华 科技中国 凤凰 新闻100 新浪 创头条 中国教育文化 搜狐环球 中国发展报道 创始人联网 中信网 数字e家 知乎 今日头条 朝闻天下中国发展产业研究网 哔哩哔哩 市场导报 东方今报 。
8.2020年12月,《海丰乡音(第29期)》杂志載文:《砥砺前行,探秘洞悉堂奥 ——记创立 Yang-Hilbert型不等式理论的杨必成教授》(建成文).
9.2021年1月6日,《盘点2020年数学家杨必成教授成果篇》一文在下列20家 :
媒体发布:人民政协 中国科学 华夏访谈 媒体中国 朝闻天下 凤凰新闻 中国发展报道 广东广播电视台 创头条 中国信息 中华人物榜 哔哩哔哩 百度百家 12小时新闻 中国创投 民族品牌 博客中国 科技中国 搜狐 东方工匠。
10. 2021年1月10日《今日头条》(诗文寻真)載文《汕尾轿子杨必成总结年度科研成果,汕尾名医、诗人吕烈题诗祝贺》。
11. 2021年1月5日。获聘为“中国未来研究会科技分会第四届理事(2021-2025)”证书。
12. 2021年3月8日,《自由探秘 成果斐然— 记创立Yang-Hilbert型不等式理论的杨必成教授》发表于下列24家网站:
中国访谈 中国科学 中华 创头条 网易 中国快报 新华热线 中宏新闻 凤凰 中国教育文化 第一科技 中国财经 朝闻天下 创始人联网 中国教育新闻 新浪 人民观察 百度百家 简书 法治与社会 科技观察 中青新闻 中国信息 中讯网。
13. 2021年4月7日,《“寒门”是如何出贵子 —记革命伉俪杨耿仪郑芸的育儿之道》,发表于下列24家网站:
中国访谈 中华人物榜 今日头条 网易 中国教育科学 朝闻天下 媒体中 腾讯 中华网 华夏小康 凤凰 华夏文学 知乎 幸福生活 国企网 央视在线 朝闻天下 中红网 创头条 法治与社会 百度百家 中国教育文化 新浪 新时代人物。
14. 2021年4月,入册《走近大国倔起的开拓者》(80-81页)(中国未来研究会科技分会编).
15. 2021年8月20日,《我是科学人》栏目视频:“杨必成:执于探微,不负数学一生”上挂7家网站:人民日报 央视频 腾讯 优酷 爱奇艺 bilibili 微博。
16. 2021年8月30日,《中国数学家杨必成 执于探微 不负数学一生》挂23家网站:
人民日报 中华网 中国访谈 中国教育 新浪 中国信息 网易 第一资讯 百度 百家 第一资讯 中新资讯 中华新闻网 国际新闻网 科技焦点网 中国焦点网 每日资讯网 大众导报网 前沿科技网 中华科技网 中国城市网 每日财经网 广东新闻网 中国教育新闻网。
17. 2021年9月18-19日,杨必成应邀参加了在“北京会议中心”举行的“第十九届中国科学家(国际)论坛”,荣获大会组委会等颁发的《“十四五”科技强国创新驱动领军人物》证书及奖牌。
18. 2021年9月21-22日,汕尾电视台报道:《杨必成:白首穷经,忘我求知的数学家》。
19. 2021年10月19日,《我是科学人》栏目视频:《杨必成:执于探微,不负数学一生》获挂2网站:学习强国,西部影视。
20. 2021年12月16日,《数学家杨必成的“老三届”情结》刊載如下21个网站:
CCTV华夏之声 中国高新科技 今日头条 凤凰 科学头条 中研科技 中华新闻网 中国快报网 前沿科技网 科技焦点网 搜狐 中国教育新闻 中国焦点网 中新资讯网 中华科技网 经济周刊 第一资讯网 新浪 腾讯 百度百家网易。
21.2021年10月,《执于探微,不负数学一生——访广东第二师范学院应用数学研究所所长,教授杨必成》入册《中国力量》(528-536页)(中国文化交流协会编,光明日报出版社出版)。
22. 2022年2月16日,“杨必成:疫情中的2021盘点”刊載如下28个门户网站:人民日报客户端 CCTV华夏之声 中国战略产业 中华网 中研科技 中华新闻 前沿科技 百度百家 中华科技 中国看点 中国快报 中国城市 国际新闻 科技焦点 经济周刊 中国教育之家 中国焦点 前瞻科技 中国文化 中新资讯 爱科学 中国晨报 科技周刊 每日资讯 中国教育新闻 第一资讯 广东新闻 中国高新科技。
23. 2022年4月,入册《聚焦新时代的中国学者》(72-73页)并获该书特邀编委(中国未来研究会科技分会编)。
24. 2022年9月,《宝剑锋从磨砺出---记汕尾籍数学家杨必成教授》刊于《时代潮人》2022,2:35-41.
25. 2022年9月,《宝剑锋从磨砺出---记汕尾籍数学家杨必成教授》经下列25个网站转载:
中国高新科技 中国焦点日报 中国产业新闻 东方工匠 网易 简书 今日头条 知乎 UC头条 华人号 财经参考报 中国文化 豆瓣 中国西南新闻 中国看点 南方头条 搜狐 CCTV华夏之声 新时代先锋 中国双创 新浪宝剑 腾讯 中国小康新闻 百度百家 新时代人物
26. 杨必成入册于2022年10月10日发布的斯坦福大学版“全球前2%顶尖科学家”的“终身影响力排行版(1960-2021)”榜单。
27. 2022年10月,文《执于探微,“数”写精彩人生——记广东第二师范学院应用数学研究所所长杨必成教授》入册《喜迎二十大 奋进新征程》一书(153-154页。中国人文科学出版社).

三.吕烈新曲及附注
2022年10月16日,杨必成教授同窗好友吕烈医师作曲如下:
[中吕__魔合罗带过最高楼]
祝杨必成教授获全球前2%顶尖科学家殊荣(注1)
少年未得东风便(注2),青灯破万卷(注3)。
十年冷凳磨穿(注4),一身壮志痴缠(注5)。
勘开参量风云转(注6),旱地掘穿甘露泉(注7)。
文章如井喷,论著忽等身(注8)。
[最高楼] 仰看前路山尖,绚丽辉煌迫近。
回观撒下花籽,五彩缤纷一片(注9)。
注1. 2022年10月10日,杨必成入册美国斯坦福大学John P.A. Ioannidis 教授团队发布的“全球前2%顶尖科学家”的“终身影响力排行版(1960-2021年)”榜单。
注2. 1958年后,杨必成因受父亲历史寃案所累及文革災祸,求学之路一波三折,下乡时险遭雷击致死,身心倍受创伤。
注3. 杨必成下乡时竟自学了《微积分》,练就一身“杀龙”本领。
注4. 从1958入读初中到1998年升任教授,杨必成整整坐了40年冷板凳。
注5. 杨必成一生沉迷于数学梦中,天天思考数学问题,以至不能自拔。
注6. 1998年,在头痛病痊愈后第4年,杨必成突发奇想,引入独立参量,在美国数学家帮助下,在国际上发表了推广希尔伯特积分不等式的研究论文。
注7. 之后多年,杨必成的发表成果终于填补了该领域60多年的理论空白,创立了杨一希尔伯特不等式理论 (《科技日报》2013年语)。
注8. 杨必成至今己发表数学研究论文580多篇,出版论著13部,参编专著17部(20章),总字数超过一千万字。
注9:吕烈注:杨教授建立数学研究所,培养了一批批的数学人材,写下多篇高质量的论文,被国內外发表推介,多人因此而评上教授。
总注:获入册全球前2%顶尖科学家榜单随想。
荣幸。逆境图存,呕心枥血, 四十年磨一剑,入围榜单值得!
有憾。这次,杨必成仅有241篇国外发表论文获参评,有300多篇发表在祖国大地的中文论文,13本中英文专著及18本参编专著成果未获参评,故所得评分不够理想。
无悔。自发表数学论文至今30多年来,杨必成既不把论文及专著全写在国外,也不全写在国内,然而第一篇重要论文及第一本专著却发表在国内,这一做法适合于他一生的科研抉择!
杨必成胞弟杨建成点赞:这次中国入选数学家144人,中国人口14亿人,平均每一千万人中才有一人上榜。数学家杨必成的入选,是我们杨氏家族的光荣与骄傲。

附:杨必成教授个人简历:
杨必成,男,1946年8月出生于广东汕尾市城区,1966年6月毕业于汕尾中学高中,1968年12月下乡到海丰公平公社当知青,1975年12月回城当民办教师,1977年底以数学满分(200分)的高考成绩入读华南师范大学数学系本科班,1982年1月大学毕业,获理学士学位,分配到广东教育学院数学系任助教。他长期从事函数论的教学与研究,于1998年评为数学教授,曾任广东教育学院数学系主任(1999~2007年)兼学院党委委员,全国不等式研究会理事长(2009~2013年),现任广东第二师范学院应用数学研究所所长(2006年至今),兼任全国不等式研究会顾问,中山大学国家数字家庭工程技术研究中心兼职教授,汕尾中学广州校友会会长(2019年~)。多年来,他被聘为多家国际数学杂志编委,及美国《数学评论》、德国《数学文摘》评论员。
他于1986年开始发表数学论文,至今一直从事可和性,算子理论与解析不等式理论的基础应用研究。1998年,他在国际SCI数学期刊《数学分析及应用(JMAA)》发表论文,引入独立参量,推广Hilbert积分不等式;他还在《美国数学会会刊(PAMS)》发表论文,建立加强型的Hardy-Hilbert不等式,其最佳内常数因子联系Euler常数;2004年,他引入两对共轭指数辅以独立参量,首倡参量化数学思想方法,建立推广的Hardy-Hilbert型不等式及其算子刻画理论,即Yang-Hilbert不等式理论(《科技日报》2013年语),解决了Hardy-Hilbert型不等式理论的推广难题,填补了该领域60多年(1934-1997年)的理论空白;2016年至今,他与团队成员一起努力拼搏,建立起12个门类Hilbert型不等式最佳常数因子联系多参数的等价陈述,从而完善了Yang-Hilbert不等式理论。应用上,他创建了大量Hilbert型不等式,使其最佳常数因子联系上著名的Reimann -zeta函数,丰富了Reimann-zeta函数的理论内涵;他还应用改进的Euler-Maclaurin求和公式,建立新型的联系部分和的Hardy-Hilbert不等式,并拓展到创建多类半离散及积分型不等式中去。杨必成业已在国内外数学期刊发表论文560多篇(其中195篇为SCI收录,17篇刊登在《数学学报》、《数学年刊》、《数学进展》等中文权威期刊上),并在中国科学出版社及国外Springer等科学出版社出版专著13部。此外,他还参编Springer等出版社出版专著18部,含22章理论内容。
2002年,他应邀参加“2002-国际数学家大会”(北京),获15分钟发言;2008年,他应邀参加“第五届非线性分析国际会议”(美国),获45分钟发言。他曾连续13次获广东第二师范学院“科研贡献奖”(2003~2015年);据《2009年版中中国期刊高被引指数》一书记载:2003-2007年发表论文于2008年引用频次,全国数学类前20名排名,杨必成名列第二;2007年底,他被广东省教育工会授予“广东省师德先进个人”荣誉称号; 2010年,“美国国际传记中心”授予他“2010年度世界风云人物”纪念金牌;他的科研事迹2次入编《中华人民共和国年鉴(2013, 2018年卷)》; 2014年,他被评为“汕尾当代名人”;2015年,他荣获“科学中国人2014年度人物奖”,“2015年度中国科技创新突出贡献人物奖”,及“2015年度中国教育创新创业领军人物奖”; 2016年,他的事迹获入编新版《世界名人录(第三卷)》;2016年3月,他获英国剑桥国际传记中心颁以“Most Influential Scientists of 2016”(2016年度最具影响力科学家)银质奖盘;2017年2月,他获英国剑桥国际传记中心颁以“Leading Scientists of the Word~ 2017~”(2017年度世界顶尖科学家)荣誉证书;2019年获“建国70周年 中国科技创新杰出人物”证书;2021年,杨必成参加第十九届中国科学家论坛,被授予“十四五”科技强国创新驱动领军人物”荣譽奖牌;2021年10月,科技部 “我是科学人”栏目组,录制了介绍数学家杨必成教授的采访视频,挂上了《学习强国》等网站。最近,杨必成教授入册于2022年10月10日发布的斯坦福大学“全球前2%顶尖科学家”的“终身影响力排行版(1960-2021)”榜单。
2005年至今,《人民日报》、《科技日报》、《祖国》、《汕尾日报》及《中国科技网》等100多家报刊、杂志、网站陆续报道了他的科研业绩。
杨必成教授的座右铭是:“志存高远,脚踏实地,勤勉治学,执于探微”。
免责声明:市场有风险,选择需谨慎!此文仅供参考,不作买卖依据。
标签:
-
 回观撒下花籽,五彩缤纷一片——记数学家杨必成: 疫情三年科研成果丰硕 2023年春,肆虐在祖国大地三年的新冠疫情终于划上了句号。回望这段艰难的时光,杨必成教授及其科研团队成员逆境而上,坚持组织好课题研究,
回观撒下花籽,五彩缤纷一片——记数学家杨必成: 疫情三年科研成果丰硕 2023年春,肆虐在祖国大地三年的新冠疫情终于划上了句号。回望这段艰难的时光,杨必成教授及其科研团队成员逆境而上,坚持组织好课题研究, -
 坚持安全、高品质,优可舒洗脸柔巾及消毒湿巾标准获评企业标准“领跑者” 近日,亚太(广州)日用品有限公司(以下简称亚太)企业标准Q APC002-2022《柔巾》及企业标准Q APC001-2022《消毒湿巾》,以旗下优可舒品牌
坚持安全、高品质,优可舒洗脸柔巾及消毒湿巾标准获评企业标准“领跑者” 近日,亚太(广州)日用品有限公司(以下简称亚太)企业标准Q APC002-2022《柔巾》及企业标准Q APC001-2022《消毒湿巾》,以旗下优可舒品牌 -
 南阳东大肛肠医院 专注百姓胃肠肛肠健康的正规医疗机构 南阳东大肛肠医院 专注百姓胃肠肛肠健康的正规医疗机构胃肠、肛肠疾病是目前生活中较为高发的一种疾病,它的出现给患者所带来的危害是尤为
南阳东大肛肠医院 专注百姓胃肠肛肠健康的正规医疗机构 南阳东大肛肠医院 专注百姓胃肠肛肠健康的正规医疗机构胃肠、肛肠疾病是目前生活中较为高发的一种疾病,它的出现给患者所带来的危害是尤为 -
 从人脉到流量,中小企业玩转数字升级轻松获客需要多久? 产品高速迭代,企业日新月异,工业品行业风起云涌,在这个慢进则退的时代,中小企业如何才能洞察每一个有价值的新风口,在同行竞争中大获全
从人脉到流量,中小企业玩转数字升级轻松获客需要多久? 产品高速迭代,企业日新月异,工业品行业风起云涌,在这个慢进则退的时代,中小企业如何才能洞察每一个有价值的新风口,在同行竞争中大获全 -
 “开放北京的活力与动力”招商推介系列活动外资专场成功举办 为更大力度吸引和利用外资,做好外资企业服务,推动更多外资项目落地,3月16日,北京市投资促进服务中心以‘智’汇赋能,共享...
“开放北京的活力与动力”招商推介系列活动外资专场成功举办 为更大力度吸引和利用外资,做好外资企业服务,推动更多外资项目落地,3月16日,北京市投资促进服务中心以‘智’汇赋能,共享... -
 匠心之选,营养相伴 ——皇室澳玛儿中老年配方羊奶粉全新上市 目前,我国中老年人群基数不断扩大,而这一人群的健康和营养意识也在不断提升,银发一族市场也迎来巨大发展机遇。成人奶粉重在功能细化,不
匠心之选,营养相伴 ——皇室澳玛儿中老年配方羊奶粉全新上市 目前,我国中老年人群基数不断扩大,而这一人群的健康和营养意识也在不断提升,银发一族市场也迎来巨大发展机遇。成人奶粉重在功能细化,不
-
 回观撒下花籽,五彩缤纷一片——记数学家杨必成: 疫情三年科研成果丰硕 2023年春,肆虐在祖国大地三年的新冠疫情终于划上了句号。回望这段艰难的时光,杨必成教授及其科研团队成员逆境而上,坚持组织好课题研究,
回观撒下花籽,五彩缤纷一片——记数学家杨必成: 疫情三年科研成果丰硕 2023年春,肆虐在祖国大地三年的新冠疫情终于划上了句号。回望这段艰难的时光,杨必成教授及其科研团队成员逆境而上,坚持组织好课题研究, -
 坚持安全、高品质,优可舒洗脸柔巾及消毒湿巾标准获评企业标准“领跑者” 近日,亚太(广州)日用品有限公司(以下简称亚太)企业标准Q APC002-2022《柔巾》及企业标准Q APC001-2022《消毒湿巾》,以旗下优可舒品牌
坚持安全、高品质,优可舒洗脸柔巾及消毒湿巾标准获评企业标准“领跑者” 近日,亚太(广州)日用品有限公司(以下简称亚太)企业标准Q APC002-2022《柔巾》及企业标准Q APC001-2022《消毒湿巾》,以旗下优可舒品牌 -
 南阳东大肛肠医院 专注百姓胃肠肛肠健康的正规医疗机构 南阳东大肛肠医院 专注百姓胃肠肛肠健康的正规医疗机构胃肠、肛肠疾病是目前生活中较为高发的一种疾病,它的出现给患者所带来的危害是尤为
南阳东大肛肠医院 专注百姓胃肠肛肠健康的正规医疗机构 南阳东大肛肠医院 专注百姓胃肠肛肠健康的正规医疗机构胃肠、肛肠疾病是目前生活中较为高发的一种疾病,它的出现给患者所带来的危害是尤为 -
 从人脉到流量,中小企业玩转数字升级轻松获客需要多久? 产品高速迭代,企业日新月异,工业品行业风起云涌,在这个慢进则退的时代,中小企业如何才能洞察每一个有价值的新风口,在同行竞争中大获全
从人脉到流量,中小企业玩转数字升级轻松获客需要多久? 产品高速迭代,企业日新月异,工业品行业风起云涌,在这个慢进则退的时代,中小企业如何才能洞察每一个有价值的新风口,在同行竞争中大获全 -
 “开放北京的活力与动力”招商推介系列活动外资专场成功举办 为更大力度吸引和利用外资,做好外资企业服务,推动更多外资项目落地,3月16日,北京市投资促进服务中心以‘智’汇赋能,共享...
“开放北京的活力与动力”招商推介系列活动外资专场成功举办 为更大力度吸引和利用外资,做好外资企业服务,推动更多外资项目落地,3月16日,北京市投资促进服务中心以‘智’汇赋能,共享... -
 匠心之选,营养相伴 ——皇室澳玛儿中老年配方羊奶粉全新上市 目前,我国中老年人群基数不断扩大,而这一人群的健康和营养意识也在不断提升,银发一族市场也迎来巨大发展机遇。成人奶粉重在功能细化,不
匠心之选,营养相伴 ——皇室澳玛儿中老年配方羊奶粉全新上市 目前,我国中老年人群基数不断扩大,而这一人群的健康和营养意识也在不断提升,银发一族市场也迎来巨大发展机遇。成人奶粉重在功能细化,不 - 孔达达榜书艺术探索:知本法正 气韵穆穆 书法,是世界艺术之林中,最为独特的一门艺术。它是文字符号、形象艺术、意象艺术多重结合的典范代表,也是最能体现数千年延绵不绝的中华文
-
 你知道废弃塑料怎么再生利用吗? 废塑料的再生利用可分为简单再生利用和改性再生利用两大类,简单再生利用是指将回收的废塑料制品经过分类、清洗、破碎、造粒后直接加工成型
你知道废弃塑料怎么再生利用吗? 废塑料的再生利用可分为简单再生利用和改性再生利用两大类,简单再生利用是指将回收的废塑料制品经过分类、清洗、破碎、造粒后直接加工成型 -
 超燃直播,爱采购带你直奔生意场! 免责声明:市场有风险,选择需谨慎!此文仅供参考,不作买卖依据。
超燃直播,爱采购带你直奔生意场! 免责声明:市场有风险,选择需谨慎!此文仅供参考,不作买卖依据。 -
 首届点淘“我为贵州毕节代言”新星选拔赛圆满落幕 推动乡村振兴和数字中国战略,深化粤黔东西部协作,深入挖掘毕节人才资源,扎实推进毕节产业电商发展,提升毕节好物好景影响力,2月22日至3
首届点淘“我为贵州毕节代言”新星选拔赛圆满落幕 推动乡村振兴和数字中国战略,深化粤黔东西部协作,深入挖掘毕节人才资源,扎实推进毕节产业电商发展,提升毕节好物好景影响力,2月22日至3 -
 广西玉林:持续深化打假打私体系建设 为经济运行稳中提质保驾护航 近年来,广西玉林市烟草专卖局持续深化“政府领导、部门联合、多方参与、密切协作”的打假打私体系建设,与各职能部门联合开展“岁末年...
广西玉林:持续深化打假打私体系建设 为经济运行稳中提质保驾护航 近年来,广西玉林市烟草专卖局持续深化“政府领导、部门联合、多方参与、密切协作”的打假打私体系建设,与各职能部门联合开展“岁末年... -
 热讯:域潇集团海口摘地 建区域总部 记者从海口江东新区管理局获悉,海南域潇锆钛控股股份有限公司(以下简称“域潇”)继本月初在海口江东新区成交一块人才公寓用地后,3月...
热讯:域潇集团海口摘地 建区域总部 记者从海口江东新区管理局获悉,海南域潇锆钛控股股份有限公司(以下简称“域潇”)继本月初在海口江东新区成交一块人才公寓用地后,3月... -
 道森新能源高端装备制造基地落户南通 总投资10亿元 3月16日,道森股份(603800 SH)发布公告称,公司控股子公司洪田科技有限公司(“洪田科技”)拟与江苏省南通港闸经济开发区管委会签订《合...
道森新能源高端装备制造基地落户南通 总投资10亿元 3月16日,道森股份(603800 SH)发布公告称,公司控股子公司洪田科技有限公司(“洪田科技”)拟与江苏省南通港闸经济开发区管委会签订《合... -
 【世界独家】微软发布新脚本,可修复 WinRE BitLocker 绕过漏洞
IT之家3月17日消息,微软于今天发布了新脚本,可以让用户轻松修复Windows恢复环境(WinRE)中的BitLocker绕过安全漏洞。下载
【世界独家】微软发布新脚本,可修复 WinRE BitLocker 绕过漏洞
IT之家3月17日消息,微软于今天发布了新脚本,可以让用户轻松修复Windows恢复环境(WinRE)中的BitLocker绕过安全漏洞。下载 -
 世界热门:中集世联达上海总部落地北外滩 今天,中集世联达上海总部“回家”入驻北外滩签约仪式在白玉兰广场举办。虹口区正在加快产业集聚、人才集聚,不断提升楼宇经济发展能级...
世界热门:中集世联达上海总部落地北外滩 今天,中集世联达上海总部“回家”入驻北外滩签约仪式在白玉兰广场举办。虹口区正在加快产业集聚、人才集聚,不断提升楼宇经济发展能级... -
 快讯:小米 Redmi Note 12 Turbo 手机全球首发第二代骁龙 7+ 处理器
IT之家3月17日消息,在今日下午的高通骁龙新品发布会上,第二代骁龙7+处理器正式发布。IT之家从发布会现场获悉,小米Redmi品牌总经理卢伟冰
快讯:小米 Redmi Note 12 Turbo 手机全球首发第二代骁龙 7+ 处理器
IT之家3月17日消息,在今日下午的高通骁龙新品发布会上,第二代骁龙7+处理器正式发布。IT之家从发布会现场获悉,小米Redmi品牌总经理卢伟冰 -
 世界热资讯!三星Galaxy Watch 5/Pro在菲律宾上线血压监测和ECG心电图
IT之家3月17日消息,三星GalaxyWatch5系列具有多种健康和健身追踪功能,包括血压监测、ECG心电图、心率监测、睡眠追踪、SpO2
世界热资讯!三星Galaxy Watch 5/Pro在菲律宾上线血压监测和ECG心电图
IT之家3月17日消息,三星GalaxyWatch5系列具有多种健康和健身追踪功能,包括血压监测、ECG心电图、心率监测、睡眠追踪、SpO2 -
 今日热议:【家在绿水青山畔】信阳市固始县孙滩村:绘就强村富民新画卷 阳春三月,柔和的微风吹拂着大地。豫西南的大山深处,长江河畔,信阳市固始县陈淋子镇孙滩村坐落于此。艳阳当空,这个依山而建的村庄尚...
今日热议:【家在绿水青山畔】信阳市固始县孙滩村:绘就强村富民新画卷 阳春三月,柔和的微风吹拂着大地。豫西南的大山深处,长江河畔,信阳市固始县陈淋子镇孙滩村坐落于此。艳阳当空,这个依山而建的村庄尚... -
 天天日报丨综述:日本专家认为美欧紧缩货币政策埋下金融隐患 新华社东京3月16日电综述:日本专家认为美欧紧缩货币政策埋下金融隐患新华社记者刘春燕受美国硅谷银行关闭风波等因素影响,欧洲三大股市...
天天日报丨综述:日本专家认为美欧紧缩货币政策埋下金融隐患 新华社东京3月16日电综述:日本专家认为美欧紧缩货币政策埋下金融隐患新华社记者刘春燕受美国硅谷银行关闭风波等因素影响,欧洲三大股市... -
 世界头条:郎溪经开区:抢抓春日“黄金期”按下项目建设“加速键” 一年之计在于春。近期,郎溪经开区抢抓连日来的晴好天气,抖擞干劲,分秒必争,确保重点项目建设再提速、再突破。在安徽同创顶立机械有...
世界头条:郎溪经开区:抢抓春日“黄金期”按下项目建设“加速键” 一年之计在于春。近期,郎溪经开区抢抓连日来的晴好天气,抖擞干劲,分秒必争,确保重点项目建设再提速、再突破。在安徽同创顶立机械有... -
 主播DIY双层LCD显示器:显示效果媲美OLED
IT之家3月17日消息,YouTube主播MatthewPerks近日DIY了一台双层LCD显示器,希望通过叠加的方式来达到OLED
主播DIY双层LCD显示器:显示效果媲美OLED
IT之家3月17日消息,YouTube主播MatthewPerks近日DIY了一台双层LCD显示器,希望通过叠加的方式来达到OLED -
 全球百事通!亚马逊海外购心愿单即将下线
IT之家3月17日消息,据多名IT之家网友收到的电子邮件显示,亚马逊海外购心愿单将于2023年3月24日之前下线,亚马逊提醒用户尽快查看心愿
全球百事通!亚马逊海外购心愿单即将下线
IT之家3月17日消息,据多名IT之家网友收到的电子邮件显示,亚马逊海外购心愿单将于2023年3月24日之前下线,亚马逊提醒用户尽快查看心愿 -
 南阳东大肛肠医院口碑怎么样,收费贵不贵,一切以事实说话 南阳东大肛肠医院口碑怎么样,收费贵不贵,一切以事实说话南阳东大肛肠医院是一家正规专业的肛肠专科医院,市医保定点医院,坚持医疗过程透明
南阳东大肛肠医院口碑怎么样,收费贵不贵,一切以事实说话 南阳东大肛肠医院口碑怎么样,收费贵不贵,一切以事实说话南阳东大肛肠医院是一家正规专业的肛肠专科医院,市医保定点医院,坚持医疗过程透明 -
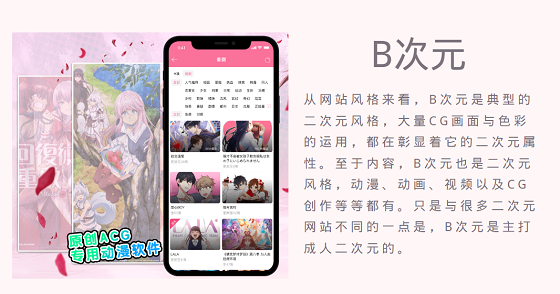 先是半次元,这次今日头条又要收购B次元?动漫二次元当红平台表示不能忍! 近期,国内二次元圈爆出一个大新闻,图文大佬今日投票要收购二次元平台B次元了。该事件不断发酵,并在互联网上引发诸多议论。不少人网友震
先是半次元,这次今日头条又要收购B次元?动漫二次元当红平台表示不能忍! 近期,国内二次元圈爆出一个大新闻,图文大佬今日投票要收购二次元平台B次元了。该事件不断发酵,并在互联网上引发诸多议论。不少人网友震 -
 云米智能家居懂生活,也更加懂你 把家务交给云米全屋智能之后,下班回到家的生活就剩了两个字:舒适。分享3款云米科技智能家电,用过的人都说:太香啦!忘带钥匙、丢钥匙大
云米智能家居懂生活,也更加懂你 把家务交给云米全屋智能之后,下班回到家的生活就剩了两个字:舒适。分享3款云米科技智能家电,用过的人都说:太香啦!忘带钥匙、丢钥匙大 - 科锐国际 | 集成电路行业:车载芯片市场前景广阔,研发类人才供不应求 在刚刚落幕的2023年全国两会上,集成电路行业成为代表们讨论的重点之一。作为我国经济发展的战略性、基础性和先导性产业,集成电路行业关系
-
 秋葵怎么判断熟了 秋葵摸起来黏黏的是坏了吗? 秋葵怎么判断熟了若是采摘的时候,则适宜在落花后四天采摘,有个头还嫩,秋葵就是食用嫩果的,而且花后采摘要及时。最佳采收时间就是花开败
秋葵怎么判断熟了 秋葵摸起来黏黏的是坏了吗? 秋葵怎么判断熟了若是采摘的时候,则适宜在落花后四天采摘,有个头还嫩,秋葵就是食用嫩果的,而且花后采摘要及时。最佳采收时间就是花开败 -
 无花果可以在家里种吗 无花果到底是不是凶树? 无花果可以在家种。无花果对环境的适应能力比较强,能开花结果而且具有观赏性,很适合在家里种植。在庭院里种植无花果树时需要准备比较空旷
无花果可以在家里种吗 无花果到底是不是凶树? 无花果可以在家种。无花果对环境的适应能力比较强,能开花结果而且具有观赏性,很适合在家里种植。在庭院里种植无花果树时需要准备比较空旷 -
 治疗湿疹的最好方法有什么 湿疹不治疗会自愈吗? 治疗湿疹的最好方法有什么?湿疹是一类比较常见的皮肤性疾病,很多患者认为湿疹并没有那么严重,所以不去治疗,但是时间长了就会引起更为严
治疗湿疹的最好方法有什么 湿疹不治疗会自愈吗? 治疗湿疹的最好方法有什么?湿疹是一类比较常见的皮肤性疾病,很多患者认为湿疹并没有那么严重,所以不去治疗,但是时间长了就会引起更为严 -
 茅台酱香品牌赖茅上线喜酒新品 看匠心之作如何抢占喜宴C位? 古言:无酒不成席,宾客参加喜宴也可以被称为喝喜酒。随着消费升级、年轻群体渐成消费主力,加之健康生活理念的转变,人们在喜宴上的消费水
茅台酱香品牌赖茅上线喜酒新品 看匠心之作如何抢占喜宴C位? 古言:无酒不成席,宾客参加喜宴也可以被称为喝喜酒。随着消费升级、年轻群体渐成消费主力,加之健康生活理念的转变,人们在喜宴上的消费水 -
 环球视点!淘宝直通车溢价怎么设置?设置多少合适? 其实很多开直通车的运营者们都希望好好了解直通车溢价这一操作,把这个操作好了,可能就能够为店铺的商品带来更好的排名,开始具体要怎...
环球视点!淘宝直通车溢价怎么设置?设置多少合适? 其实很多开直通车的运营者们都希望好好了解直通车溢价这一操作,把这个操作好了,可能就能够为店铺的商品带来更好的排名,开始具体要怎... -
 b站创作激励计划收益如何计算?附注意事项 越来越多的up主都加入了进来,享受这平台给与的权益。这其中肯定会有一些新人up主,在关于激励计划收益会有各种问题。那么b站收益是怎...
b站创作激励计划收益如何计算?附注意事项 越来越多的up主都加入了进来,享受这平台给与的权益。这其中肯定会有一些新人up主,在关于激励计划收益会有各种问题。那么b站收益是怎... -
 乳胶漆刷完后多久可以开窗通风 刷乳胶漆阴干还是开窗? 乳胶漆刷完后多久可以开窗通风乳胶漆刷完后一般三到五天可以开窗通风。具体开窗通风时间需要根据房屋的温度以及漆膜的厚度进行调整,例如在
乳胶漆刷完后多久可以开窗通风 刷乳胶漆阴干还是开窗? 乳胶漆刷完后多久可以开窗通风乳胶漆刷完后一般三到五天可以开窗通风。具体开窗通风时间需要根据房屋的温度以及漆膜的厚度进行调整,例如在 -
 消息!京东快车普通推广与海投区别在哪? 目前京东商城有很多商家开店是都会用到一些付费推广工具的,对于一些新手来说,这些推广工具种类太多了,从而导致分不清它们的功能了...
消息!京东快车普通推广与海投区别在哪? 目前京东商城有很多商家开店是都会用到一些付费推广工具的,对于一些新手来说,这些推广工具种类太多了,从而导致分不清它们的功能了... -
 如何使眼睛自然变大 使眼睫毛变长的小妙招有什么? 如何使眼睛自然变大你没有看错,是的是自然变大,不是通过手术去割双眼皮,开眼角等方法。前几天小编就在网上看到一个超神奇的化妆术,相信
如何使眼睛自然变大 使眼睫毛变长的小妙招有什么? 如何使眼睛自然变大你没有看错,是的是自然变大,不是通过手术去割双眼皮,开眼角等方法。前几天小编就在网上看到一个超神奇的化妆术,相信 -
 神探笔记电影结局什么意思 神探笔记结尾凶手是谁? 神探笔记电影结局什么意思1、袁理跟纹身男是一伙的,袁初是纹身男杀的嫁祸给周耀明,但警察没证据抓到周耀明,袁理为了让周再次杀人露出马
神探笔记电影结局什么意思 神探笔记结尾凶手是谁? 神探笔记电影结局什么意思1、袁理跟纹身男是一伙的,袁初是纹身男杀的嫁祸给周耀明,但警察没证据抓到周耀明,袁理为了让周再次杀人露出马 - “蜜壶汁”和4维空间润滑油女用选什么更好? 眼看这个三月已经过去一半了,算下来四舍五入三分之一年就过去了呀。所以这几天蜜壶大郎就盘算了一下,您年到目前为止被问咨询得最多的问题是
-
 阳台朝西好还是朝东好 阳台在左边好还是右边好? 阳台朝西好还是朝东好1、阳台朝东是比较好的。2、道家有讲紫气东来之说,所以在东方就是象征着有祥瑞之气的地方,所以选择坐西朝东是让东面的
阳台朝西好还是朝东好 阳台在左边好还是右边好? 阳台朝西好还是朝东好1、阳台朝东是比较好的。2、道家有讲紫气东来之说,所以在东方就是象征着有祥瑞之气的地方,所以选择坐西朝东是让东面的 -
 环球新消息丨京东新人省省卡怎么取消?如何使用? 现在京东新人省省卡是平台推出的一款购物省钱措施,开通的用户能够获得一定的优惠红包,然后在平台上买东西的时候进行抵扣。那么京东...
环球新消息丨京东新人省省卡怎么取消?如何使用? 现在京东新人省省卡是平台推出的一款购物省钱措施,开通的用户能够获得一定的优惠红包,然后在平台上买东西的时候进行抵扣。那么京东... -
 女儿写给母亲节妈妈的祝福有哪些 母亲给女儿的祝福语简短 女儿写给母亲节妈妈的祝福有哪些1、昨天我遇到天使在淋雨,我便把雨伞借给了她,今天她问我是要荣华还是富贵,我说什么都不要,只要现在看
女儿写给母亲节妈妈的祝福有哪些 母亲给女儿的祝福语简短 女儿写给母亲节妈妈的祝福有哪些1、昨天我遇到天使在淋雨,我便把雨伞借给了她,今天她问我是要荣华还是富贵,我说什么都不要,只要现在看 -
 重庆动物园大熊猫反向参观游客 重庆动物园有多少只熊猫? 重庆动物园大熊猫反向参观游客近日,有网友在重庆动物园看大熊猫时拍到有趣一幕。视频中,大熊猫坐在木桥上,双手悠闲搭在护栏,看着周围游
重庆动物园大熊猫反向参观游客 重庆动物园有多少只熊猫? 重庆动物园大熊猫反向参观游客近日,有网友在重庆动物园看大熊猫时拍到有趣一幕。视频中,大熊猫坐在木桥上,双手悠闲搭在护栏,看着周围游 -
 河南国企有哪些 适合女生能进国企的专业有哪些? 河南国企有哪些1、食品行业:双汇、众品、大用、志元食业、永达鸡、华英鸭、三全、思念、白象、科迪、南街村、莲花味精、王守义十三香、金
河南国企有哪些 适合女生能进国企的专业有哪些? 河南国企有哪些1、食品行业:双汇、众品、大用、志元食业、永达鸡、华英鸭、三全、思念、白象、科迪、南街村、莲花味精、王守义十三香、金 -
 翡翠玉镯有裂纹时间久怎么办 有裂的翡翠手镯能戴吗? 翡翠玉镯有裂纹时间久怎么办1、如果是轻度的裂纹,不影响正常佩戴,那么只要在平时的佩戴过程中要小心,避免碰撞就可以了,如果已经影响美
翡翠玉镯有裂纹时间久怎么办 有裂的翡翠手镯能戴吗? 翡翠玉镯有裂纹时间久怎么办1、如果是轻度的裂纹,不影响正常佩戴,那么只要在平时的佩戴过程中要小心,避免碰撞就可以了,如果已经影响美 -
 世界热点!Steam 开启史上首次春季特卖,多款游戏大作迎来新史低
IT之家3月17日消息,Steam游戏商城于今日开启了史上首次春季特卖,该特卖取代了之前的农历新年特卖,并成为了新的四大季节性特卖之一。本次特
世界热点!Steam 开启史上首次春季特卖,多款游戏大作迎来新史低
IT之家3月17日消息,Steam游戏商城于今日开启了史上首次春季特卖,该特卖取代了之前的农历新年特卖,并成为了新的四大季节性特卖之一。本次特 -
 上海普陀发布15项民心工程和为民办实事项目 2023年预计新增养老床位250张 3月16日,上海市普陀区举行2023年养老服务工作会议暨民心工程和为民办实事项目启动发布会,15项“2023年普陀区民心工程和为民办实事项目...
上海普陀发布15项民心工程和为民办实事项目 2023年预计新增养老床位250张 3月16日,上海市普陀区举行2023年养老服务工作会议暨民心工程和为民办实事项目启动发布会,15项“2023年普陀区民心工程和为民办实事项目... -
 【环球热闻】崇明这个项目相当于在岛上种了556万棵树,建了5个森林公园 3月13日,长兴岛热电有限责任公司10万吨级燃煤燃机二氧化碳捕集与利用(CCUS)项目进入全面正式运行阶段,江南造船集团成为首家通过管道输送用
【环球热闻】崇明这个项目相当于在岛上种了556万棵树,建了5个森林公园 3月13日,长兴岛热电有限责任公司10万吨级燃煤燃机二氧化碳捕集与利用(CCUS)项目进入全面正式运行阶段,江南造船集团成为首家通过管道输送用 -
 寻踪探迹,“泉”力出击——甘肃酒泉消防出征全省消防救援队伍火灾调查暨新闻岗位... 3月16日至19日,甘肃省消防救援队伍火灾调查暨新闻宣传岗位练兵比武竞赛在天水市秦州区举行,来自全省15个支队的135名业务骨干代表队同台竞技
寻踪探迹,“泉”力出击——甘肃酒泉消防出征全省消防救援队伍火灾调查暨新闻岗位... 3月16日至19日,甘肃省消防救援队伍火灾调查暨新闻宣传岗位练兵比武竞赛在天水市秦州区举行,来自全省15个支队的135名业务骨干代表队同台竞技 -
 微资讯!dv摄像机品牌(dv摄像机哪个牌子好) 1、在日常生活中,人们往往想记录一些精彩的瞬间,但是用数码相机记录下来的瞬间都是静止无声的,无法真正感受到当时激动人心的
微资讯!dv摄像机品牌(dv摄像机哪个牌子好) 1、在日常生活中,人们往往想记录一些精彩的瞬间,但是用数码相机记录下来的瞬间都是静止无声的,无法真正感受到当时激动人心的 -
 碧生源小贴士:出汗多,不一定能减肥 很多人都相信减肥就要多出汗的说法,这让很多人在运动的时候,一定要出一身汗,甚至用上了裹保鲜膜、穿厚衣服等等办法,好像只有这样才能让
碧生源小贴士:出汗多,不一定能减肥 很多人都相信减肥就要多出汗的说法,这让很多人在运动的时候,一定要出一身汗,甚至用上了裹保鲜膜、穿厚衣服等等办法,好像只有这样才能让 -
 在美甲行业这股热潮下,穿戴甲的机会在哪里? 近年来,伴随着消费升级和爱美意识的觉醒,人们对美的追求边界越来越广泛,对变美产品的挑选越来越精细化,而手是女人的第二张脸这句话已经深深
在美甲行业这股热潮下,穿戴甲的机会在哪里? 近年来,伴随着消费升级和爱美意识的觉醒,人们对美的追求边界越来越广泛,对变美产品的挑选越来越精细化,而手是女人的第二张脸这句话已经深深
热门资讯
-
 回观撒下花籽,五彩缤纷一片——记数学家杨必成: 疫情三年科研成果丰硕 2023年春,肆虐在祖国大地三年的新...
回观撒下花籽,五彩缤纷一片——记数学家杨必成: 疫情三年科研成果丰硕 2023年春,肆虐在祖国大地三年的新... -
 坚持安全、高品质,优可舒洗脸柔巾及消毒湿巾标准获评企业标准“领跑者” 近日,亚太(广州)日用品有限公司...
坚持安全、高品质,优可舒洗脸柔巾及消毒湿巾标准获评企业标准“领跑者” 近日,亚太(广州)日用品有限公司... -
 南阳东大肛肠医院 专注百姓胃肠肛肠健康的正规医疗机构 南阳东大肛肠医院 专注百姓胃肠肛...
南阳东大肛肠医院 专注百姓胃肠肛肠健康的正规医疗机构 南阳东大肛肠医院 专注百姓胃肠肛... -
 从人脉到流量,中小企业玩转数字升级轻松获客需要多久? 产品高速迭代,企业日新月异,工业...
从人脉到流量,中小企业玩转数字升级轻松获客需要多久? 产品高速迭代,企业日新月异,工业...
观察
图片新闻
-
 精选!崖州区举行2023年春季新兵入伍欢送仪式 光荣启程 逐梦军营 3月15日,崖州区举行2023年上半年...
精选!崖州区举行2023年春季新兵入伍欢送仪式 光荣启程 逐梦军营 3月15日,崖州区举行2023年上半年... -
 三亚天涯区用好红色资源为新兵上入营“第一课” “我志愿去西藏服兵役” 一直以来,天涯区人武部注重征兵宣...
三亚天涯区用好红色资源为新兵上入营“第一课” “我志愿去西藏服兵役” 一直以来,天涯区人武部注重征兵宣... -
 三亚天涯区举行2023年春季新兵入伍欢送仪式 又是一年送兵日,热血男儿赴征程。...
三亚天涯区举行2023年春季新兵入伍欢送仪式 又是一年送兵日,热血男儿赴征程。... -
 “巾帼红”引领“文明风” 三亚“半边天”“创文”显身手 三亚明佳园林环卫集团吉阳三队的女...
“巾帼红”引领“文明风” 三亚“半边天”“创文”显身手 三亚明佳园林环卫集团吉阳三队的女...
精彩新闻
-
 国产剧情探索类游戏《十五》上线 Steam 页面,穿越回 90 年代
IT之家3月17日消息,由国产游戏开...
国产剧情探索类游戏《十五》上线 Steam 页面,穿越回 90 年代
IT之家3月17日消息,由国产游戏开... -
 “寻味溧阳 鲜享一步”顺丰速运春茶寄递推介会在溧阳举办 3月16日,寻味溧阳 鲜享一步顺丰...
“寻味溧阳 鲜享一步”顺丰速运春茶寄递推介会在溧阳举办 3月16日,寻味溧阳 鲜享一步顺丰... -
 刷新世界纪录,中广核岭澳核电站 1 号机组连续安全运行 6000 天
IT之家3月17日消息,据中国广核集...
刷新世界纪录,中广核岭澳核电站 1 号机组连续安全运行 6000 天
IT之家3月17日消息,据中国广核集... -
 “数字生命卡”众筹产品材质被换?《流浪地球 2》导演郭帆回应
3月17日消息,赛凡科幻空间近期发...
“数字生命卡”众筹产品材质被换?《流浪地球 2》导演郭帆回应
3月17日消息,赛凡科幻空间近期发... -
 当前热文:三亚海棠区三个土地流转项目成交额250万余元 3月16日,记者从海棠区农业农村局...
当前热文:三亚海棠区三个土地流转项目成交额250万余元 3月16日,记者从海棠区农业农村局... -
 全球资讯:华硕预告 ROG AM5 主板最高可支持 192GB 内存
IT之家3月17日消息,华硕预告AM5平...
全球资讯:华硕预告 ROG AM5 主板最高可支持 192GB 内存
IT之家3月17日消息,华硕预告AM5平... -
 精选!崖州区举行2023年春季新兵入伍欢送仪式 光荣启程 逐梦军营 3月15日,崖州区举行2023年上半年...
精选!崖州区举行2023年春季新兵入伍欢送仪式 光荣启程 逐梦军营 3月15日,崖州区举行2023年上半年... -
 热点在线丨“虹吸”京沪?杭州离一线还有多远 先是放话“吸走北京上海人才”,紧...
热点在线丨“虹吸”京沪?杭州离一线还有多远 先是放话“吸走北京上海人才”,紧... -
 江西一萤石矿采场发生冒顶 4人被困 3月17日,江西省吉安市新干县新衡...
江西一萤石矿采场发生冒顶 4人被困 3月17日,江西省吉安市新干县新衡... -
 企业那么喜欢客服外包,原因竟是…… 很多人会问,客服的招聘管理应该很...
企业那么喜欢客服外包,原因竟是…… 很多人会问,客服的招聘管理应该很... -
 三亚天涯区举行2023年春季新兵入伍欢送仪式 又是一年送兵日,热血男儿赴征程。...
三亚天涯区举行2023年春季新兵入伍欢送仪式 又是一年送兵日,热血男儿赴征程。... -
 广西推动“快递进村”向“快递出村”升级 3月16日,记者从广西壮族自治区邮...
广西推动“快递进村”向“快递出村”升级 3月16日,记者从广西壮族自治区邮... -
 “巾帼红”引领“文明风” 三亚“半边天”“创文”显身手 三亚明佳园林环卫集团吉阳三队的女...
“巾帼红”引领“文明风” 三亚“半边天”“创文”显身手 三亚明佳园林环卫集团吉阳三队的女... -
 【世界聚看点】国网宁夏电力公司4项成果获奖 )第二届宁夏职工创新成果评选结果...
【世界聚看点】国网宁夏电力公司4项成果获奖 )第二届宁夏职工创新成果评选结果... -
 忠诚担当筑警魂 守护平安不停歇 牡丹江市公安局东安分局江南第二派...
忠诚担当筑警魂 守护平安不停歇 牡丹江市公安局东安分局江南第二派... -
 全球动态:发挥优势多方发力恢复和扩大消费——访市商务局市场运行和消费促进处处长... 本报记者郑微政府工作报告把“着力...
全球动态:发挥优势多方发力恢复和扩大消费——访市商务局市场运行和消费促进处处长... 本报记者郑微政府工作报告把“着力... -
 科学家发现大规模量产 OLED 面板的溶液处理方案
IT之家3月17日消息,韩国釜山国立...
科学家发现大规模量产 OLED 面板的溶液处理方案
IT之家3月17日消息,韩国釜山国立... -
 三亚天涯区用好红色资源为新兵上入营“第一课” “我志愿去西藏服兵役” 一直以来,天涯区人武部注重征兵宣...
三亚天涯区用好红色资源为新兵上入营“第一课” “我志愿去西藏服兵役” 一直以来,天涯区人武部注重征兵宣... -
 当前速读:System76推出Meerkat mini Linux PC:最高第12代处理器
IT之家3月17日消息,System76于今...
当前速读:System76推出Meerkat mini Linux PC:最高第12代处理器
IT之家3月17日消息,System76于今... -
 全球消息!印度1新郎不满新娘“成绩太差”退婚,女方家人抖惊人真相 结婚需要经过多方考虑,可能因为观...
全球消息!印度1新郎不满新娘“成绩太差”退婚,女方家人抖惊人真相 结婚需要经过多方考虑,可能因为观... -
 淘宝一个钻多少钱?五钻多少钱? 在淘宝,无论是买家帐号还是卖家...
淘宝一个钻多少钱?五钻多少钱? 在淘宝,无论是买家帐号还是卖家... -
 社会热议 苗博士开启鸟类保护万里行湖北站活动 3月15日,苗博士播时盾鸟类保护万...
社会热议 苗博士开启鸟类保护万里行湖北站活动 3月15日,苗博士播时盾鸟类保护万... -
 世界快看点丨中国人寿寿险黑龙江省分公司打造品质理赔服务 近年来,中国人寿寿险黑龙江省分公...
世界快看点丨中国人寿寿险黑龙江省分公司打造品质理赔服务 近年来,中国人寿寿险黑龙江省分公... -
 【环球播资讯】谷歌发现三星调制解调器存在18个漏洞:知道手机号码就可发起攻击
... IT之家3月17日消息,谷歌ProjectZe...
【环球播资讯】谷歌发现三星调制解调器存在18个漏洞:知道手机号码就可发起攻击
... IT之家3月17日消息,谷歌ProjectZe... -
 世界今亮点!垣曲:羊肚菌抢“鲜”上市 丰收迎来好“钱”景 山西运城市垣曲县以建设黄河流域生...
世界今亮点!垣曲:羊肚菌抢“鲜”上市 丰收迎来好“钱”景 山西运城市垣曲县以建设黄河流域生... -
 人人学急救 急救为人人 30余名市民群众 练“救”真本领 学员正在进行“CPR+AED”实践考核...
人人学急救 急救为人人 30余名市民群众 练“救”真本领 学员正在进行“CPR+AED”实践考核... -
 环球观速讯丨北京石景山推出“石惠十条” 北京市石景山区近日发布了《石景山...
环球观速讯丨北京石景山推出“石惠十条” 北京市石景山区近日发布了《石景山... - 品质铸就品牌 匠心铸就未来 和锐之旗一起“质”敬匠心豫企 随着国民经济的不断增长,消费升级...
-
 天天观天下!国家发展改革委:多项措施巩固防疫成果 抓紧补齐重点环节防控设施短板 据中央广播电视总台中国之声《新闻...
天天观天下!国家发展改革委:多项措施巩固防疫成果 抓紧补齐重点环节防控设施短板 据中央广播电视总台中国之声《新闻... -
 天天热头条丨英国商业贸易部携团赴三亚开展经贸交流合作 深化务实合作 实现共赢发展 3月16日下午,海南自由贸易港(三...
天天热头条丨英国商业贸易部携团赴三亚开展经贸交流合作 深化务实合作 实现共赢发展 3月16日下午,海南自由贸易港(三... -
 全球速讯:Amazfit发布42mm GTR Mini智能手表
IT之家3月17日消息,AmazfitGTR4于...
全球速讯:Amazfit发布42mm GTR Mini智能手表
IT之家3月17日消息,AmazfitGTR4于... -
 江苏徐州:救急救困 稳岗稳企 政策 “及时雨”守护民生“烟火味” “这笔钱帮我们度过暂时难关,缓解...
江苏徐州:救急救困 稳岗稳企 政策 “及时雨”守护民生“烟火味” “这笔钱帮我们度过暂时难关,缓解... -
 天天简讯:谷歌 Pixel 7a 原型现身eBay拍卖网站:无法启动,遗失SIM卡托盘
IT之家3月17日消息,名为“nikosko...
天天简讯:谷歌 Pixel 7a 原型现身eBay拍卖网站:无法启动,遗失SIM卡托盘
IT之家3月17日消息,名为“nikosko... -
 环球观速讯丨三亚崖州湾科技城开设“绿色通道” 搭建政企会客厅 架起服务连心桥 “大家提出的建议和诉求,我们现场...
环球观速讯丨三亚崖州湾科技城开设“绿色通道” 搭建政企会客厅 架起服务连心桥 “大家提出的建议和诉求,我们现场... -
 三星公布Galaxy A34/A54 5G手机支持寿命:5年安全更新
IT之家3月17日消息,三星公司日前...
三星公布Galaxy A34/A54 5G手机支持寿命:5年安全更新
IT之家3月17日消息,三星公司日前... -
 西藏自治区今年力争文化产业产值增长15%以上 3月16日,全区文化工作会议在拉萨...
西藏自治区今年力争文化产业产值增长15%以上 3月16日,全区文化工作会议在拉萨... -
 今日最新!市政务服务中心拓宽办事诉求渠道 “未办成事”协调服务窗口帮群众解难题 办理政务服务事项时遇到因政策调整...
今日最新!市政务服务中心拓宽办事诉求渠道 “未办成事”协调服务窗口帮群众解难题 办理政务服务事项时遇到因政策调整... -
 环球短讯!上海迪士尼年卡停售,续卡不受影响
IT之家3月17日消息,上海迪士尼度...
环球短讯!上海迪士尼年卡停售,续卡不受影响
IT之家3月17日消息,上海迪士尼度... -
 2023海南自由贸易港(三亚)楼宇经济专题推介会在西安举行 3月16日,2023海南自由贸易港(三...
2023海南自由贸易港(三亚)楼宇经济专题推介会在西安举行 3月16日,2023海南自由贸易港(三... -
 江苏徐州:政策“精准滴灌”产业链,引千亿金融“活水”润实体经济 本报记者陈羿帆党的二十大报告更加...
江苏徐州:政策“精准滴灌”产业链,引千亿金融“活水”润实体经济 本报记者陈羿帆党的二十大报告更加... -
 董仲舒的天人合一什么意思 天人合一是谁提出的? 董仲舒的天人合一什么意思董仲舒的...
董仲舒的天人合一什么意思 天人合一是谁提出的? 董仲舒的天人合一什么意思董仲舒的... -
 江苏徐州:小银杏“乘风破浪”勇出海,精准服务助力特色农产品“卖全球” 3月16日,在徐州国利银杏制品有限...
江苏徐州:小银杏“乘风破浪”勇出海,精准服务助力特色农产品“卖全球” 3月16日,在徐州国利银杏制品有限... -
 法国时间与北京时间相差多久 法国早上9点中国几点? 法国时间与北京时间相差多久中国北...
法国时间与北京时间相差多久 法国早上9点中国几点? 法国时间与北京时间相差多久中国北... -
 热固性塑料和热塑性塑料如何检测? 塑料的种类分多种,常用的早已占据...
热固性塑料和热塑性塑料如何检测? 塑料的种类分多种,常用的早已占据... -
 嘉霖浦厨卫荣膺2022国际设计大奖 闪耀世界舞台 MUSE Design Awards(缪斯设计奖...
嘉霖浦厨卫荣膺2022国际设计大奖 闪耀世界舞台 MUSE Design Awards(缪斯设计奖... -
 铁观音是指什么茶 铁观音的传说之一王说是指什么? 铁观音是地地道道的乌龙茶。传统工...
铁观音是指什么茶 铁观音的传说之一王说是指什么? 铁观音是地地道道的乌龙茶。传统工... -
 婴儿奶粉哪个品牌的好?佳贝艾特向扬,用五优营养羊奶粉领头力量 据调查数据显示:我国儿童超重肥胖...
婴儿奶粉哪个品牌的好?佳贝艾特向扬,用五优营养羊奶粉领头力量 据调查数据显示:我国儿童超重肥胖... -
 山东蓬莱有什么好玩的 山东蓬莱旅游攻略和费用 山东蓬莱有什么好玩的1、蓬莱阁蓬...
山东蓬莱有什么好玩的 山东蓬莱旅游攻略和费用 山东蓬莱有什么好玩的1、蓬莱阁蓬... -
 价格空前“内卷”,传祺价值为王,多重钜惠助力汽车消费 3月,全国消费促进月正式开启,各...
价格空前“内卷”,传祺价值为王,多重钜惠助力汽车消费 3月,全国消费促进月正式开启,各... -
 普希金写致大海的写作背景是什么 普希金是哪个国家的? 普希金写致大海的写作背景是什么《...
普希金写致大海的写作背景是什么 普希金是哪个国家的? 普希金写致大海的写作背景是什么《...